INTRODUCTION

The aim of this study is to provide an overview of mathematical modeling used to solve problems involving fractions while engaging in angle model. We understand an angle model as a representation using an angle of a geometrical shape such as a circle or line to help visualize operations involving fractions. For example a fraction such as 3/4 can be represented using an angle model as 270^o/360^o. When angle model is used, it allows that all the fractions under consideration are expressed using one unit before they are added, subtracted, multiplied or divided. The other models might bring this view but it is hidden. Operation involves adding, subtraction, dividing and multiplying numbers. However, in this study we looked into addition only. The study aimed to show how addition of fractions can be presented to those who see the use of symbols or other models as a challenge. This work presents some ideas and developments of major importance to practitioners working in the field of mathematics education. It also seeks to improve the teaching and learning of fractions which tries to develop a teaching strategy by showing the role of modeling and applications in everyday mathematics teaching. Challenges are faced by both learners and teachers when they do operations involving fractions. Many authors support the view that fractions are a problem to learners. For example, Clarke et al. (2007) reveal that misperception in teaching and learning fractions is obvious when students cannot blend fraction problems in their textbooks with what they experience in their daily life. It is most likely that challenges in operations with fractions are attributed to the fact that fractions need to be interpreted in many ways as Kieren (1980) suggests and many models represent fractions as only useful for one role. According to Kieren (1980), fractions can be used to represent; a part-whole, a measure, a quotient (division), an operator or a ratio. In all these interpretations models can be used and this places a teacher at an advantage since they end up with sufficient pedagogical content knowledge and content knowledge useful for teaching and learning. According to Shulman (1987), pedagogical content knowledge and content knowledge are an amalgam of content and pedagogy and of mathematical content knowledge respectively. These types of knowledge and other types Shulman (1987) mentions determine the approach trainee teachers use when on school based studies or when tasked to solve fraction problems during class activity.

The approaches surrounding how trainee teachers compute fractions using traditional mathematical algorithm of teaching and learning (TMATL) is provided. Bishara (2015) understands TMATL as an approach whereby teaching and learning is teacher centered and the learner is required to passively receive mathematical knowledge. The failure of a TMATL lens anchored on the behaviourist theory to allow trainee teachers engage in all the interpretations of fractions provided above paved way to use the reformed mathematical algorithm for teaching and learning mathematics (RMATL). The use of a RMATL brought an angle model. RMATL is what Bishara (2015) refer to as active learning. RMATL is premised on; social interaction, active participation of the learner, curriculum used is adapted to learners’ context, use of learning and teaching materials which are diverse and embracive of multicultural views. The use of a model during operations of fractions is supportive of the premises of RMATL. RMATL is in support of the tenets of constructivism and this allows cognitive constructive to be discussed. Cognitive constructivism as a theory of learning will be discussed and will be used to support the emerging literature related to fractions.

FRACTIONS

The concept of fractions originated the time humankind started to measure (Bereznai, 1999) certain quantities such as length, mass, time and this is in support of the idea that fractions can be used to measure as Kieren (1980) proposes. Unlike counting which yields discrete data, measurement is an activity which is more precise, removes disorder, reduces waste, ensures openness and fairness and the National Measurement System (2009) is in support. This explains why the data from measurement is continuous. Measurement using fractions first came with Greeks (Gillings, 1972) and when the Egyptians encountered fractions they used only unit fractions most probably because it is easy to partition to equal parts which can be used to measure. A unity fraction always has a numerator of one.

For example

3/4 = 1/4 + 1/4 + 1/4 or

3/4 = 1/2 + 1/4

The above way of expressing fraction as a unity fraction is symbolic modelling. One can also refer to it as decomposition of the given fraction into unit values whose sum is equal to the given fraction. Also, it might be referred to as a student invented algorithm and echoes very well with ideas in RMATL mentioned above.

Even though the student invented algorithm mentioned has some tenets of RMATL, it does not allow a learner to master operations of fractions. This might be because knowledge of fractions gained still remains inert. Hale (2013) understands inert knowledge as knowledge which cannot be applied in daily activities. Also, sometimes the decomposition or modelling of fractions using symbolic values is a challenge to learners. This requires one to engage other strategies of modelling to enable a learner see that a fraction represent a; part-whole, measure, quotient (division), operator or ratio Kieren (1980) recommends as useful. When dealing with fractions many conceptual ideas related to fraction use come into play which the learner or teacher needs to know or reinforce in order to successfully perform operations with fractions. One needs to see if the fractions under consideration have the same denominator or they do not have. The idea of same denominator is what many mathematics textbooks refer to as equivalent. Patilla (2003) replaces the idea of equivalent with sameness and this might allow learner to understand why we need to change fractions before we perform an operation when models are used. If they do not have the same denominator then one needs to first change the fraction so that they are expressed using the same units. When they have different denominators, the fractions being added are like adding kilograms and grams or adding quantities expressed in different units. We need to change physical quantities measured in different units so that they are expressed using the same unit, grams or kilograms. Fractions expressed using different denominators are like a physical quantity such as mass expressed in different units. When denominators in fractions are made equivalent, it enables fractions with the same denominator to be added or subtracted. The process of changing given fractions to have the same denominator comes as a challenge. However, such challenges sometimes are minimal when models are used.

MATHEMATICAL MODEL

According to Bassanezi (1994), he suggests that there is no single definition of the term mathematical model and this makes confusion about a model. Different people have different opinions on what a mathematical model is. However, our position of the definition of a model is that from Frigg (2006) who opines that a model denotes to a simplified and stylized form of the part or feature of the world that we are interested in (the so-called ‘target system’). Surfacing a mathematical model to use in solving a mathematical problem is a cognitive activity. Sekerák (2010) categorizes modelling as a learning environment in which students are required to inquire or scrutinize through the use of mathematics circumstances from other areas to provide solutions to certain given problems. Thus, the importance of incorporation of situations from everyday life and other areas of knowledge in the classroom plays a fundamental role. With the aim to enable learners to intervene in this reality aligns this strategy to the cognitivist theory of learning to be discussed in sections which will follow. From the view of Barbosa (2003) a model is a construction of a mathematical artefact in a learning environment emerging when students are tasked to inquire and/or explore by means of mathematical situations arising in other areas of knowledge. According to Abramowitz and Stegun (1968) the importance of a model is to describe behaviour qualitatively or quantitatively. When a model answers the question how, it is of the qualitative type and when it answers the question how much it is of the quantitative type.

Abramowitz and Stegun (1968) consider four stages of activity in modelling namely; building, studying, testing and use of the model. In support of stages required in mathematical modelling, Sekerák (2010) identifies three stages engaged during modelling. The stages are: identification of model situation starting points, construction of a mathematical model and verification of the built model.

The identification stage as the first stage entails deciding which input information is applicable and this has some tenets of the building stage. In this phase competence dealing with information plays an important function. In the second stage with characteristics of the building, studying and testing stages, the teacher builds the model and tests validate as Abramowitz and Stegun (1968) suggest before demonstrating to the learners. The final stage, the verification entails checking if the model is in communication with the real situation which you are dealing with.

According to Sekerák (2010), different types of models exist. These are: arithmetic which is represented using an operation table, algebraic which engages in algebraic equations of any type, graphical uses of a graph in which variables are shown on the axis, geometrical uses geometrical figures and when combined, will integrate some or all the other types. The geometrical model combined with a mathematical representation is the one that this study used to represent fractions. To show how addition and subtraction of fractions can be used in easing the challenges which learners face using angle model in this study, a circle or a line is used. On account of the approach solving the how question, the model is of the qualitative type. Using a circle or a line to present the fraction of degrees represented by the given fraction is an invented activity/strategy encouraged in RMATL.

Invented strategies are methods used in teaching and learning mathematics so that the learner does not see the concept taught as abstract but instead becomes concrete as he cognitively engages in solution finding. Cuoco et al. (1996) in support of use of invented strategies opine that inventing is done for specific purpose and this requires one with certain habits of mind. The mentioned authors emphasize the need of people involved in mathematics to have some geometric and arithmetic habits of mind which then enable them to invent (Cuoco et al., 1996) or to come up with solutions to certain given mathematical problems. Engaging with such activities determines the learning theories used. These might be the behaviourist and cognitivist teaching and learning theory on which the TMATL and RMATL are anchored on respectively.

Learning Theories

Two teaching and learning theories will be discussed. These are the cognitive constructivist and the behaviourist. These are not from the same camp so they ensure that each theory of teaching and learning flourish

Behaviourist Teaching and Learning Theory

In TMATL discussed above, the mathematical skill development needed in an operation is achieved through use of the behaviourist. TMATL epitomizes behaviourism. Drilling is used to change the behaviour of the learner. Orton (2004) suggests that in behaviourism, ‘...Exposition by the teacher followed by practice of skills and techniques is a feature which most people remember when they think of how they learned mathematics’ (p. 29). Orton further goes on to explain that while the objective is to create strong stimulus-response links, as teachers well know, these are regularly passing – having a ‘use it or lose it’ impermanence – and uses the example of the addition of fractions, the algorithm of which is taught, re-taught, and practiced throughout early schooling only to be forgotten repeatedly as some are not adapted or related to a model.

Cognitivist Teaching and Learning Theory

Cognitivism arose largely in reply to behaviourism, with learning seen as an adaptive process where knowledge may be transferred between individuals but is stored as inner mental concepts or images. Social cognitivism, which recognizes that learning, is at least as much a social activity as it is behavioural and cognitive, fuses elements of behaviourism and cognitivism with social aspects of learning (Bandura, 1986). Bandura’s (1986) theory emphasizes the reputation of observational learning, by which behavioural and/or cognitive changes are brought about by the learner’s comparative observations of others and of self, a process merged in the concept of self-efficacy beliefs (Bandura, 1997), which have a prominent role in the learning activities of math-averse students (Klinger, 2009).

The cognitivist teaching and learning theory emphasizes that cognitive processes such as thinking, problem solving, language, concept formation and information processing are crucial in teaching and learning (Snelbecker, 1983). According to Ertmer and Newby (2013) cognitivists are rationalist since their view is knowledge acquisition is a mental activity that necessitates inside coding and arranging from the part of the learner. The learner is viewed as a very active participant in the learning process. The real focus of the cognitive approach is on changing the learner by encouraging him/her to use appropriate learning strategies. This then is in line with the use of mathematical model which comes with some strategies to observe and describe, observe and explain and finally to observe and predict.

The properties of cognitivist teaching and learning theory discussed above where students engage with invented methods reflects what happens in a classroom where RMATL is used. According to Boaler (2002) mathematics teachers engaging with RMATL enables learners to use mathematics learnt at school in situations outside the classroom. This is not the only significance of engaging models that allow learners to come with invented methods, some other significances of this study follow below.

Significance of the Study

When using models as an invented method, the specific purpose is to nullify or minimize the abstractness that learners encounter in mathematics concepts learning. So, one of the importance of this study is to ensure that trainee teachers understand how some of the challenges encountered when teaching fractions are solved. In Namibia for example, trainee teachers observed had challenges in the section related to addition and subtraction of fractions. Nambira et al. (2009) in support revealed that learners in Namibia have challenges when dealing with fractions. This might be attributed to trainee teachers not understanding the meaning of fractions. This problem is then carried to other sections which involve fractions and many other areas where fractions will be used. For example, Epson and Levi (2012) reveal the importance of fractions in algebra. Fractions done at lower level assist in developing algebraic thinking. The use of an angle model encourages a learner to understand processes involved when solving problems related to fractions. This led us to come up with research questions below.

Research Questions

In view of this study we asked the following questions:

(a) How can trainee teachers use the angle model in a RMATL during operations of fractions? (b) What are the perceptions of trainee teachers in the use of the angle model which engages RMATL to understand operations of fractions?

METHODOLOGY

To gain insight into the mentioned questions, a qualitative research methodology was found appropriate to use. The qualitative methodology aimed at observing, describing and explaining the process of finding the solution to a problem involving operations with fractions when the idea of angle model is engaged. The “lived experiences” from the point of view of the trainee teachers who participated were obtained from worksheets they used when they came with the invented method to solve operations of fractions (Oiler, 1982, p. 178).

The participants were seventeen trainee teachers in their third year pursuing a Bachelor of Education Honours Degree. All members of the group participated since the task of operation of fractions based on a worksheet they were given to complete during a class activity. The aim was to find out if angle model can be incorporated in their classroom activities when teaching operations of fractions had activities below.

The idea of using a worksheet with mathematical problems based on operations of fractions came as a result of observations made when trainees were failing to solve fraction problems involving addition. Observation, document analysis and interviews were used as instruments. These instruments were aimed at generating data on why trainee teachers were struggling to cope with the use of other models, line and area model used in operations of fractions. Also, the use of a number of instruments aimed at addressing reliability as this allowed to see if same results were generated from some of the instruments used and Zohrabi (2013) supports. In most cases these teachers were observed using the TMATL to get the answer of fractions which were being added or subtracted. They then pretended to have used the area or line model in their answers but in fact they would have used the TMATL strategy. After the observation and their work on worksheets they were then interviewed to generate more data for analysis.

Data analysis looked into whether the responses obtained using the area model matched values obtained when other models or approaches were used. Data gathered from interviews, observations, worksheets and analysis of documents, when combined formed the pool of text on which the qualitative research was based on. They then enabled to draw descriptions and analysis of whether the trainee teachers were aligned to the RMATL instead of the TMATL. These were in a position to represent the given fractions using angle model and then add or subtract in order to get the required answer. Besides analysing the process of conversion, the analysis also based on finding whether the stages in modelling adhered to mainly observation-gathering empirical evidence, modelling-analysing what had been observed and prediction-and extrapolating what they would have come up with. This paved way to have some findings which we have discussed below.

Presentation and Analysis of Data

The trainees managed only to solve operations of fractions involving addition in one of the lessons which they engaged. The other problems involved subtraction of fractions using angle model were done in other lessons. The presentation below shows an extract from one of the trainees who applied the angle model. This also serves as a representation of how the others also worked out. Below are samples from the worksheets showing how the trainees worked and represented the incorporation of angle model to come up with solutions for the questions on the worksheets. The problems on the worksheet that they attempted were as follows;

Use angle model to find the value of fractions added indicated below:

(a) .1/2 + 1/2 = ▢

(b) .3/4 + 1/2 = ▢

(c) .3 1/4 + 2 1/2 = ▢

Figure 1. Data Obtained from Observation of Worksheets

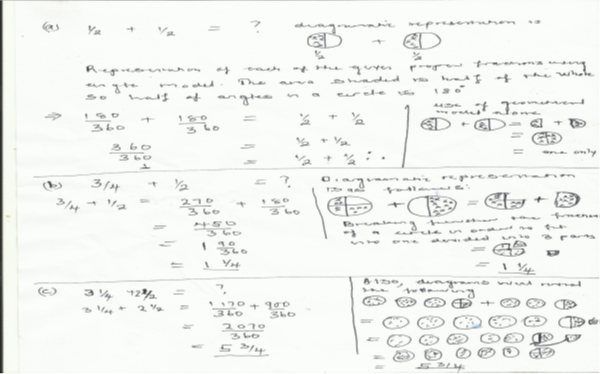
The trainee teachers managed to use the angle model in a RMATL operation with fractions. This is evidenced from observations from the worksheets they used in working out the solutions. All of them managed to come up with solution of mathematical problems which either required them to add. Subtraction, division and multiplication were done as carry home tasks and they were tasked to report their findings on whether the angle model was applicable when dealing with all operation types involving fractions. The information obtained through the use of interviews’ detail is below.

The perceptions of trainee teachers in the use of the angle model which engages RMATL to teach the operations of fractions were revealed through the interviews in which they were asked to participate. In the interview question they responded that they found the use of angle model to work problems involving fraction interesting. They indicated that when dealing with addition subtraction and division of fractions one engaged with numbers whose magnitude was not very big. However, they said when multiplying fractions using the angle model one was forced to handle numbers whose magnitude was very big.

Subtraction, division and multiplication were not done as classwork. The carry home tasks involved subtraction, division and multiplication and this was where the trainee teachers managed to extract the other comments they supplied. The theme which emerged when they were asked if the angle model was applicable to subtraction, division and multiplication confirmed the angle model as applicable to all operations. One of the trainee teachers said, “The pattern we get when using angle model to solve operation is the same with one we get when we use abstract algorithms”. Also, another idea emerging from the trainee was “Angle model operation allowed me to come up with a RMATL and besides that it enabled me not to stick to traditional approaches of providing solutions to mathematical problems”.

When interviewed as to why they did not include some geometrical diagrams in other solutions to comply with the model where a combination of geometrical and arithmetic model, they responded that they did it mentally. In support of this, Hedrén (1999) suggests that computation sometimes is done mentally while the other part of the algorithm is written or modelled. That is the geometrical figure representing each given fraction added, subtracted, multiplied or divided entailed mental construction to find how many angles represented a given fraction. To further probe whether trainees were able to see that the angle model was a type of a combinational model, they were tasked to combine the drawings of the geometric figures and the arithmetic representation.

The responses of the trainee teachers echoed with the features of the cognitivist theory of teaching and learning. In another instance they responded that the use of angle model allowed one to work with figures which were dimensionally homogeneous. This further illustrated that the strategy assisted to develop the trainees cognitively as they went to check the consistence of units they were changing.

The fact that the angle model allowed cognitive activities to be engaged was a testimony that the RMATL allows construction of knowledge not drilling of knowledge into the participants. Further evidence that the use of angle model during operations of fraction was helpful lay in that the trainee teachers fully participated in the learning activities.

Data Obtained from Interviews

The seventeen students were divided into three groups. Two groups; A and B had six students each and group C had five students. Each group was tasked to answer the interview questions shown in Table 1.

The data obtained revealed that trainee teachers can use the angle model and this was evident from what they responded appearing in column 1. It is most probably that the use of angle model allowed trainees to engage an RMATL when adding fractions. Engaging the mind actively echoes with what Ertmer and Newby (2013) suggest that knowledge acquisition is a mental activity. This led the trainee teachers to see that fractions which represent part of a whole, can be used as an operator and are useful in division (see Table 1 column 2). The data obtained during interviews was then related to data which emerged during document analysis. The view of the trainees in the use of an angle model was another model that can be used to subtract fractions. This view is supported in column 1 of Table 1. The document analysed was the mathematics syllabus. The data emerging from analysis of data is presented in Table 2.

From the data revealed in Table 2, it is evident that the trainees managed to see some of the roles fractions could play. This is evident in Table 2. The emerging of the theme of constructivist in Table 2 suggests that the trainee teachers aligned their activities to RMATL. The engagement of students in cognitive activities when they were dealing with the angle model to solve fraction problems as Snelbecker (1983) suggests allowed them to align their activities to the cognitive constructivist theory of teaching and learning. The use of models such as a glassful of water to represent a whole and a half glassful to represent a fraction seen in the syllabus encouraged trainees not to represent fractions symbolically. This was also further encouraged when the curriculum material also emphasized on the set model to solve problems related to addition of fractions. The data from document analysis, worksheets on fractions and interviews allowed us to come up with the findings to the research question.

FINDINGS

The trainees successfully used the angle model to add fractions. The worksheet in Figure 1 showed how each fraction was converted to a reading in degrees. The conversion to a degree reading allowed the trainees to see that fractions can be used for measuring. The conversion has allowed the trainees to have the same view as Kieren’s (1980) who proposes five representations of fraction and measuring is one of them.

Their perception is when an angle model is used to add fractions it comes as another alternative model to represent fractions as you add. The answer obtained when one uses an angle model is the same as when you use any other models. These findings allowed us come up with some recommendations discussed below.

RECOMMENDATION

The concept of fraction is not isolated with other concepts in mathematics. The concept of fraction is related to proportion, percentage and others. This study did not investigate how these other concepts related to fraction can also be added, subtracted, divided or multiplied when one focuses on the angle model. So there is need to direct research in that area. Also, since the angle model use focused on how fractions can be added without looking into other operations, it is also necessary to explore if the angle model can be useful in other operations which were not the center of the study. Failure of this study to look into how angle model can be used in subtraction, multiplication and division is one of its limitations.

CONCLUSION

Operation of fractions is a challenge to trainees. From what has been revealed it can be concluded that the use of angle model comes as another alternative to solve operations involving fractions and can mitigate the problem faced. The use of angle model promotes the engagement of RMATL by teachers. Also, its use allowed the unification of knowledge and skills. Different mathematical knowledge from other concepts in mathematics were engaged and also skills gained while engaging in activities related to angle model used during the process of finding the solutions of fractions.